✅ La función lineal, clave en matemáticas, se expresa como f(x)=mx+b y modela relaciones directas y proporcionales en la vida real.
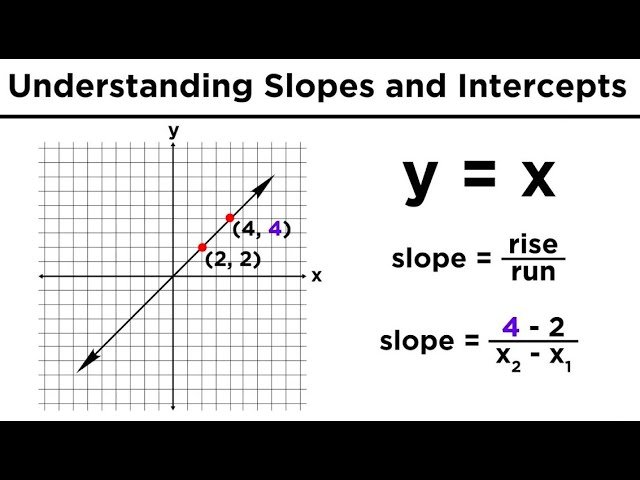
La función lineal se define generalmente como una función matemática que puede expresarse en su forma general mediante la ecuación f(x) = mx + b, donde m representa la pendiente y b la ordenada al origen o intercepto en el eje y. Esta forma permite describir una relación directa y proporcional entre dos variables, siendo uno de los conceptos básicos en álgebra y análisis matemático.
En el siguiente artículo, exploraremos detalladamente cómo se define la función lineal, cómo interpretar cada uno de sus componentes y cómo se puede usar en diferentes contextos prácticos, desde la resolución de problemas básicos hasta aplicaciones en física, economía y otras ciencias. Además, brindaremos ejemplos ilustrativos y recomendaciones para su correcta utilización y análisis.
Definición y Forma General de la Función Lineal
La función lineal en su forma general se expresa como:
f(x) = mx + b
- m (pendiente): Indica la inclinación de la recta y cómo cambia la variable dependiente f(x) respecto a la variable independiente x. Matemáticamente, es la tasa de cambio o el coeficiente de x.
- b (ordenada al origen): Es el valor de f(x) cuando x = 0, es decir, el punto donde la recta intercepta el eje y.
Interpretación de la Pendiente (m)
La pendiente m determina si la función es creciente, decreciente o constante:
- m > 0: La función es creciente; a medida que x aumenta, f(x) también aumenta.
- m < 0: La función es decreciente; a medida que x aumenta, f(x) disminuye.
- m = 0: La función es constante; f(x) = b para todo valor de x.
Uso Práctico de la Función Lineal
La función lineal es muy útil para modelar situaciones donde existe una relación proporcional o constante entre dos variables. Por ejemplo:
- Economía: Cálculo de costos fijos y variables, donde m representa el costo variable por unidad y b el costo fijo.
- Física: Movimiento rectilíneo uniforme, donde la posición cambia linealmente con el tiempo.
- Negocios: Proyección de ventas y análisis de tendencias.
Ejemplo Práctico
Supongamos que una empresa tiene un costo fijo de $5000 y un costo variable de $20 por cada producto fabricado. La función que describe el costo total (C) en función de la cantidad de productos (x) es:
C(x) = 20x + 5000
Aquí, 20 es la pendiente que indica cuánto aumenta el costo por unidad producida y 5000 es el costo fijo que la empresa debe cubrir independientemente de la producción.
Principales características y propiedades de las funciones lineales
Las funciones lineales son una de las bases fundamentales en matemática y se utilizan en una gran variedad de campos como la economía, la física, y la ingeniería. Su forma general es f(x) = mx + b, donde m representa la pendiente y b el coeficiente independiente o ordenada al origen.
Características clave
- Linealidad: La función grafica una línea recta en el plano cartesiano.
- Pendiente constante (m): Indica la tasa de cambio de la función, es decir, cómo varía el valor de y ante un cambio unitario en x.
- Intersección con el eje y (b): Es el punto donde la función cruza el eje vertical, representando el valor de y cuando x=0.
- Dominio y rango: El dominio y rango suelen ser todos los números reales (ℝ), a menos que se impongan restricciones específicas.
Propiedades fundamentales
- Adición y homogeneidad: Para cualesquiera números reales x₁, x₂ y escalares α, β, se cumple que:
f(αx₁ + βx₂) = αf(x₁) + βf(x₂). Esto refleja que la función es lineal en sentido algebraico. - Monotonía:
- Si m > 0, la función es creciente.
- Si m < 0, la función es decreciente.
- Si m = 0, la función es constante.
- Inyectividad y sobreyectividad:
- Para m ≠ 0, la función es inyectiva (no toma dos valores iguales para distintos x).
- El rango es ℝ, por lo que también es sobreyectiva sobre los reales.
Ejemplos prácticos y aplicaciones
Imaginemos que tenemos una función lineal que modela el costo mensual de un servicio de Internet, donde m = 500 representa un costo fijo por mes y b = 1000 los gastos iniciales de instalación. Entonces:
f(x) = 500x + 1000
Si un cliente usa el servicio durante 3 meses, el costo total es f(3) = 500(3) + 1000 = 2500. Aquí, la pendiente indica el incremento constante mensual, y la ordenada al origen representa el gasto inicial.
Tabla comparativa de propiedades según la pendiente
| Valor de m | Tipo de función | Comportamiento | Ejemplo |
|---|---|---|---|
| m > 0 | Creciente | Aumenta conforme x crece | f(x) = 2x + 3 |
| m < 0 | Decreciente | Disminuye conforme x crece | f(x) = -4x + 7 |
| m = 0 | Constante | Es una línea horizontal | f(x) = 5 |
Consejos para trabajar con funciones lineales
- Identificar la pendiente: Siempre que veas una ecuación, busca m para entender cómo cambia la función.
- Interpretar el coeficiente independiente: El valor de b puede tener un significado concreto, como un costo base o un valor inicial.
- Utilizar gráficos: Representar la función ayuda a visualizar su comportamiento y facilita el análisis de situaciones reales.
- Aplicar en modelos: Usar funciones lineales para aproximar fenómenos donde la relación entre variables es proporcional o constante.
Preguntas frecuentes
¿Qué es una función lineal?
Una función lineal es una relación matemática que se representa como y = mx + b, donde m es la pendiente y b es la ordenada al origen.
¿Para qué se utiliza la forma general de la función lineal?
Se usa para expresar funciones lineales de manera estándar, facilitando el análisis y la resolución de problemas.
¿Cómo se interpreta la pendiente (m) en una función lineal?
La pendiente indica la inclinación de la recta y cuánto cambia y por cada unidad que cambia x.
¿Qué representa la ordenada al origen (b)?
Es el punto donde la recta cruza el eje y, es decir, el valor de y cuando x=0.
¿Cómo se grafica una función lineal en su forma general?
Se grafica marcando el punto b en el eje y y utilizando la pendiente m para determinar otro punto con la que se traza la recta.
| Punto Clave | Descripción |
|---|---|
| Forma general | y = mx + b |
| m (pendiente) | Indica la inclinación y dirección de la recta |
| b (ordenada al origen) | Valor de y cuando x = 0 |
| Dominio | Todos los números reales |
| Rango | Todos los números reales |
| Gráfica | Una línea recta en el plano cartesiano |
| Ejemplo | y = 2x + 3 |
| Uso práctico | Modelar situaciones con cambios constantes, como costos o distancias |
¡No te olvides de dejar tus comentarios y revisar otros artículos de nuestra web que también pueden interesarte!