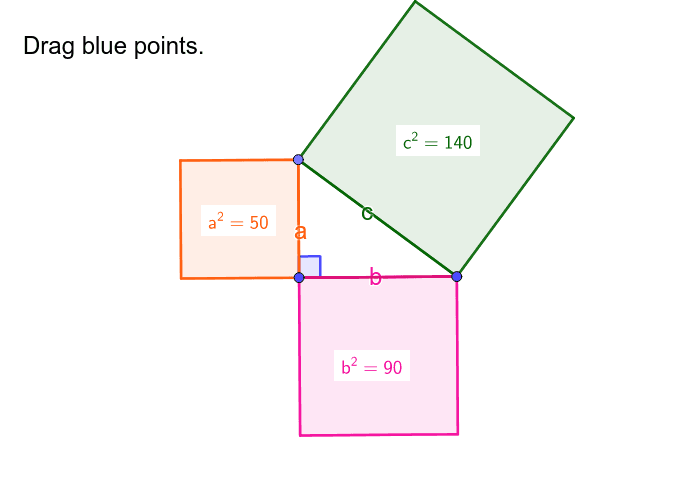
✅ El Teorema de Pitágoras afirma: en triángulos rectángulos, la suma de los cuadrados de los catetos iguala al cuadrado de la hipotenusa.
El Teorema de Pitágoras es una de las proposiciones más importantes y conocidas en matemáticas, especialmente en geometría. Este teorema establece que en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos. Matemáticamente se expresa como c² = a² + b², donde c es la hipotenusa y a y b son los catetos.
Vamos a profundizar en qué consiste el Teorema de Pitágoras, su formulación exacta y cómo se aplica en diferentes problemas matemáticos y situaciones cotidianas. Además, exploraremos ejemplos prácticos y consejos para su correcta utilización.
¿Qué es el Teorema de Pitágoras?
El Teorema de Pitágoras es una relación matemática que solo se cumple en los triángulos rectángulos, es decir, aquellos que tienen un ángulo de 90 grados. La importancia del teorema radica en que permite calcular uno de los lados del triángulo cuando se conocen los otros dos.
Su fórmula principal es:
c² = a² + b²
donde:
- c representa la longitud de la hipotenusa (el lado opuesto al ángulo recto y el más largo del triángulo).
- a y b son las longitudes de los catetos (los otros dos lados).
Ejemplo básico de aplicación
Si un triángulo rectángulo tiene catetos de longitud a = 3 y b = 4, la hipotenusa se calcula así:
c² = 3² + 4² = 9 + 16 = 25
c = √25 = 5
Esto significa que la hipotenusa mide 5 unidades.
¿Cómo se aplica el Teorema de Pitágoras en matemáticas?
El teorema tiene múltiples aplicaciones tanto en problemas teóricos como prácticos. A continuación se detallan algunas de las más comunes:
- Cálculo de distancias: En geometría analítica, permite calcular la distancia entre dos puntos en el plano cartesiano mediante la fórmula de distancia, que es una extensión del Teorema de Pitágoras.
- Construcción y diseño: Arquitectos e ingenieros lo utilizan para asegurar que estructuras tengan las medidas correctas y que los ángulos rectos sean precisos.
- Navegación y ubicación: En sistemas de posicionamiento y navegación, ayuda a determinar trayectorias rectas y distancias en mapas.
- Resolución de problemas complejos: Se usa en trigonometría y cálculo para resolver problemas que involucran triángulos y figuras más complejas.
Consejos para aplicar correctamente el teorema
- Confirma que el triángulo sea rectángulo: El teorema solo es válido si hay un ángulo de 90º.
- Identifica correctamente la hipotenusa: Es siempre el lado opuesto al ángulo recto y el más largo.
- Aplica la fórmula cuidadosamente: Eleva al cuadrado los catetos, suma esos valores y luego extrae la raíz cuadrada para obtener la hipotenusa.
- Revisa la coherencia de las unidades: Todas las medidas deben estar en las mismas unidades para evitar errores.
Ejemplos prácticos del teorema de Pitágoras en la vida cotidiana y su importancia en la resolución de problemas
El teorema de Pitágoras no es solo una fórmula abstracta que se estudia en la escuela, sino que tiene aplicaciones fundamentales en la vida cotidiana y en diversas disciplinas como la ingeniería, la arquitectura y hasta en la tecnología. A continuación, te mostramos ejemplos concretos y cómo su uso facilita la resolución de problemas prácticos.
1. Construcción y diseño arquitectónico
En el campo de la arquitectura, el teorema es esencial para calcular distancias y asegurar que las estructuras sean estables y seguras. Por ejemplo:
- Para determinar la longitud correcta de una escalera que conecta dos pisos, sabiendo la altura y la distancia horizontal.
- Calcular la diagonal de una habitación rectangular para saber la cantidad de materiales necesarios o para ubicar muebles grandes.
Ejemplo: Si una pared mide 3 metros de altura y la base de la escalera 4 metros, la longitud de la escalera será 5 metros (3² + 4² = 5²).
2. Navegación y geolocalización
En la navegación marítima o aérea, el teorema permite calcular la distancia más corta entre dos puntos, especialmente cuando se mueven en trayectorias perpendiculares.
Por ejemplo, un barco que navega 6 km hacia el norte y luego 8 km hacia el este, está a una distancia directa de:
| Trayectoria Norte (km) | Trayectoria Este (km) | Distancia Directa (km) |
|---|---|---|
| 6 | 8 | 10 (√(6² + 8²)) |
3. Tecnología y diseño gráfico
En el diseño gráfico digital, el teorema es utilizado para calcular distancias pixeladas en pantallas, ayudando a determinar la resolución y la ubicación precisa de elementos.
- Calcular la distancia entre dos puntos en una imagen para escalar o ajustar objetos.
- Determinar el tamaño de la diagonal de pantallas y dispositivos para mejorar la experiencia del usuario.
Consejos prácticos para aplicar el teorema de Pitágoras
- Identificar los catetos: Reconocer los lados perpendiculares en el problema para definir correctamente el triángulo rectángulo.
- Verificar la perpendicularidad: Asegurarse de que el ángulo de 90° esté presente para aplicar el teorema correctamente.
- Utilizar unidades consistentes: Mantener las mismas unidades (metros, centímetros) para evitar errores en el cálculo.
Importancia del teorema en la resolución de problemas
Más allá de los ejemplos prácticos, el teorema de Pitágoras es clave en la resolución de problemas matemáticos porque:
- Permite simplificar situaciones complejas en problemas de geometría y trigonometría.
- Es la base para conceptos avanzados como la distancia euclidiana en espacios multidimensionales.
- Facilita cálculos en física, como la determinación de fuerzas y trayectorias.
Preguntas frecuentes
¿Qué establece el Teorema de Pitágoras?
Establece que en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.
¿Para qué se usa el Teorema de Pitágoras?
Se utiliza para calcular la longitud de un lado en triángulos rectángulos cuando se conocen los otros dos.
¿Es aplicable solo en geometría?
No, también se aplica en física, ingeniería, informática y otras áreas que utilizan distancias o espacios.
¿Cuáles son los elementos del triángulo en este teorema?
La hipotenusa es el lado opuesto al ángulo recto y los catetos son los dos lados que forman el ángulo recto.
¿Cuál es la fórmula matemática del Teorema de Pitágoras?
Se expresa como: c² = a² + b², donde c es la hipotenusa y a y b son los catetos.
¿Se puede aplicar en triángulos que no son rectángulos?
No, solo es válido para triángulos con un ángulo de 90 grados.
| Punto Clave | Descripción |
|---|---|
| Definición | Relación entre lados en triángulos rectángulos. |
| Fórmula | c² = a² + b² |
| Hipotenusa | Lado más largo, opuesto al ángulo recto. |
| Catetos | Lados que forman el ángulo recto. |
| Aplicaciones | Matemática, física, ingeniería, arquitectura. |
| Condición | Solo para triángulos rectángulos. |
| Ejemplo práctico | Calcular la diagonal de una pantalla rectangular. |
| Historia | Atribuido a Pitágoras en la antigua Grecia. |
Te invitamos a dejar tus comentarios sobre el Teorema de Pitágoras y a explorar otros artículos en nuestra web que seguro te van a interesar.