✅ Transformá números decimales en fracciones en segundos: simplificá cuentas, mejorá tu comprensión matemática y sorprendé a todos.
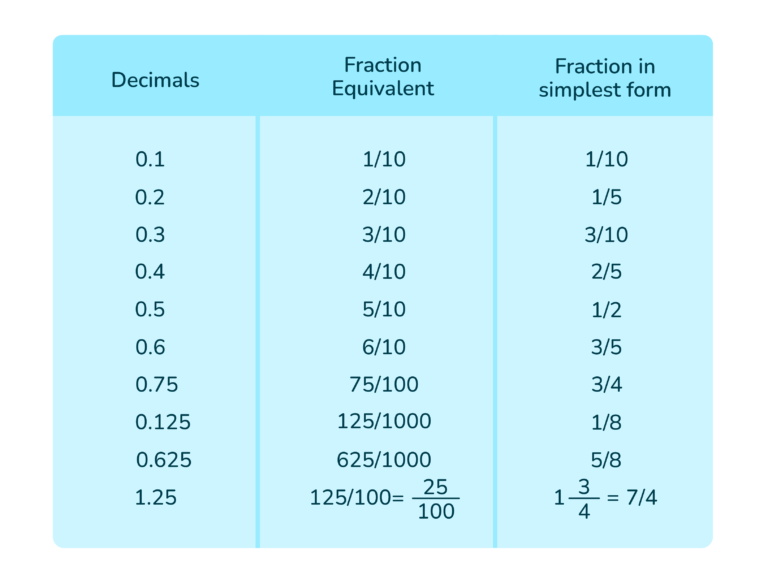
Convertir números decimales con coma a fracciones es un proceso sencillo que implica entender el valor posicional de cada dígito después de la coma y expresarlo como una fracción con denominador basado en potencias de 10. Por ejemplo, el número 3,75 se puede convertir a fracción escribiéndolo como 375/100 y luego simplificando la fracción a su forma más reducida, que es 3 3/4.
Vamos a explicar paso a paso cómo convertir cualquier número decimal con coma en su equivalente fraccionario de manera fácil y clara. Analizaremos desde los casos más básicos hasta los más complejos, ofreciendo consejos prácticos, ejemplos ilustrativos y métodos de simplificación para que puedas hacer estas conversiones sin dificultad.
Pasos para Convertir un Número Decimal con Coma a Fracción
- Escribir el número sin coma: Por ejemplo, para 4,36 escribimos 436.
- Determinar el denominador: Este será siempre una potencia de 10, dependiendo de la cantidad de cifras decimales. En el ejemplo hay dos decimales, entonces el denominador es 100.
- Formar la fracción: Colocamos el número sin coma como numerador y la potencia de 10 como denominador: 436/100.
- Simplificar la fracción: Buscamos el máximo común divisor (MCD) de numerador y denominador para reducir la fracción a sus términos más simples.
Ejemplo práctico
Convertir 2,5 a fracción:
- 2,5 = 25 (sin coma)
- Denominador = 10 (un decimal)
- Fracción inicial: 25/10
- El MCD de 25 y 10 es 5.
- Fracción simplificada: 5/2 o 2 1/2.
Consejos para Simplificar Fracciones
- Para simplificar, identifica el máximo común divisor usando métodos como la descomposición en factores primos o el algoritmo de Euclides.
- Recuerda que una fracción impropia (numerador mayor que denominador) se puede expresar como un número mixto para mayor claridad.
- En caso de decimales periódicos, la conversión es diferente y requiere otros métodos específicos.
Explicación paso a paso para transformar decimales en fracciones
Convertir un número decimal en una fracción puede parecer complicado al principio, pero con un método claro y organizado, cualquiera puede lograrlo de manera sencilla y precisa. Aquí te dejo una guía práctica paso a paso para que puedas hacerlo sin vueltas.
Paso 1: Identificar el tipo de decimal
Primero, es fundamental distinguir si el decimal es exacto (termina después de cierta cantidad de cifras) o periódico (sus cifras se repiten indefinidamente).
- Decimal exacto: 0,75; 2,5; 0,125
- Decimal periódico: 0,333… (donde el 3 se repite)
En esta sección nos centraremos en los decimales exactos, que son los más comunes y fáciles de convertir.
Paso 2: Contar la cantidad de cifras decimales
Este paso es clave para saber el denominador de la fracción. Por ejemplo, si el número es 3,456, cuenta cuántos dígitos tiene después de la coma:
- 3,456 → tres cifras decimales
Esto significa que el denominador será una potencia de 10 con el mismo número de ceros, en este caso 1000.
Paso 3: Escribir el número sin la coma como numerador
Ahora, toma el número completo sin la coma para formar el numerador:
- Para 3,456 → numerador = 3456
- Denominador = 1000 (como vimos antes)
Paso 4: Simplificar la fracción
Una vez que tengas la fracción, es importante simplificarla dividiendo numerador y denominador por su máximo común divisor (MCD).
Por ejemplo, para 3456/1000, calculamos el MCD:
| Número | Factores primos |
|---|---|
| 3456 | 2^7 × 3^3 |
| 1000 | 2^3 × 5^3 |
El MCD es 2^3 = 8, ya que es el mayor factor común. Entonces:
- Numerador simplificado: 3456 ÷ 8 = 432
- Denominador simplificado: 1000 ÷ 8 = 125
La fracción simplificada es 432/125.
Ejemplo completo con número decimal
Vamos a verlo con el número 0,625:
- Contamos las cifras decimales: tres (6, 2 y 5)
- El denominador es 10^3 = 1000
- Numerador: 625
- Fracción inicial: 625/1000
- Calculamos el MCD: 625 y 1000 tienen MCD = 125
- Dividimos ambos: 625 ÷ 125 = 5; 1000 ÷ 125 = 8
- Fracción simplificada: 5/8
Consejo práctico:
Si querés hacer este cálculo rápidamente, podés usar la técnica del mcd para simplificar la fracción manualmente o apoyarte en calculadoras que faciliten esta tarea. Además, siempre es útil verificar la fracción volviendo a dividir el numerador por el denominador para asegurarte que el resultado sea el decimal original.
Casos especiales: decimales periódicos
Para los decimales periódicos, el procedimiento es un poco distinto, ya que requieren fórmulas específicas o la representación algebraica. Por ejemplo, el decimal 0,333… se expresa como 1/3. Si te interesa, puedo explicarte este método en detalle para que puedas convertir también esos números sin problema.
Preguntas frecuentes
¿Qué es un número con coma?
Es un número decimal que utiliza la coma para separar la parte entera de la decimal, común en países de habla hispana.
¿Cómo se convierte un número decimal en fracción?
Se coloca el número sin la coma como numerador y como denominador se usa una potencia de 10 según la cantidad de cifras decimales.
¿Se pueden simplificar las fracciones resultantes?
Sí, siempre es recomendable simplificar la fracción para obtener la forma más simple posible.
¿Qué pasa si el número tiene varias cifras decimales?
Se usa una potencia de 10 con tantos ceros como cifras decimales tenga el número.
¿Es posible convertir fracciones a números decimales?
Sí, dividiendo el numerador por el denominador se obtiene el número decimal correspondiente.
Puntos clave para convertir números con coma a fracción
- Identificar la cantidad de cifras decimales del número.
- Eliminar la coma y usar el número resultante como numerador.
- Colocar como denominador una potencia de 10 según la cantidad de decimales (por ejemplo, 10, 100, 1000, etc.).
- Simplificar la fracción dividiendo numerador y denominador por su máximo común divisor.
- Verificar que la fracción sea irreducible para facilitar su comprensión.
- Recordar que números enteros son fracciones con denominador 1.
- Para números periódicos, existen métodos específicos para su conversión.
¿Te resultó útil esta guía? Dejanos tus comentarios y no olvides revisar otros artículos de nuestra web para aprender más sobre matemáticas y conversiones numéricas.