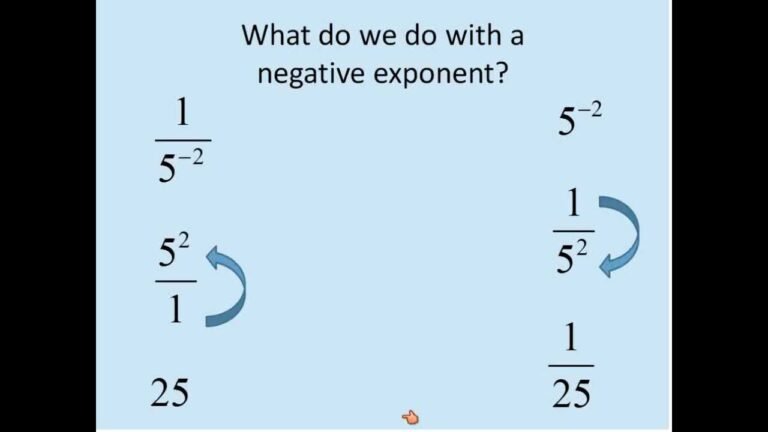✅ ¡Dominá ecuaciones complejas! Simplificá fracciones, aplicá leyes de potencias y raíces con pasos claros para resolverlas sin estrés.
Para resolver ecuaciones que contienen fracciones, potencias y raíces de manera sencilla, es fundamental seguir un proceso ordenado que permita simplificar cada elemento antes de despejar la incógnita. Esto implica conocer las propiedades básicas de las fracciones, las reglas de los exponentes y la forma correcta de trabajar con raíces cuadradas y otras raíces. Aplicando estos principios, resolverás las ecuaciones paso a paso sin confusión y con resultados precisos.
Te enseñaremos un método claro y estructurado para abordar ecuaciones con estas características. Comenzaremos explicando cómo manipular fracciones en una ecuación, luego cómo tratar potencias, y finalmente cómo trabajar con raíces. A lo largo del desarrollo, te daremos ejemplos prácticos y consejos útiles para que puedas resolver cualquier ecuación con estas operaciones de forma rápida y confiable.
1. Cómo Resolver Ecuaciones con Fracciones
Las ecuaciones con fracciones suelen ser complicadas a primera vista, pero la clave está en eliminar las fracciones multiplicando toda la ecuación por el mínimo común denominador (MCD) de todas las fracciones presentes. Esto transforma la ecuación en una sin fracciones y facilita su resolución.
- Identifica los denominadores en ambos lados de la ecuación.
- Calcula el MCD de esos denominadores.
- Multiplica toda la ecuación por el MCD para eliminar las fracciones.
- Resuelve la ecuación resultante como una ecuación algebraica común.
Por ejemplo, para resolver la ecuación 1/3 x + 2/5 = 7/15, se multiplica toda la ecuación por 15 (MCD de 3, 5 y 15), eliminando las fracciones y haciendo que la resolución sea directa.
2. Cómo Trabajar con Potencias en Ecuaciones
Para resolver ecuaciones con potencias, es fundamental conocer las propiedades de los exponentes, como la multiplicación, división y potenciación de potencias. Además, para despejar una incógnita que está elevada a una potencia, se debe aplicar la raíz correspondiente en ambos lados de la ecuación.
- Si la ecuación tiene la forma x^n = a, se debe sacar la raíz n-ésima de ambos lados para encontrar x.
- Cuando aparecen potencias en ambos lados, se puede igualar la base si las potencias son iguales.
- Es importante recordar que si la potencia es par, pueden existir dos soluciones (positiva y negativa) para la variable.
3. Cómo Resolver Ecuaciones que Involucran Raíces
Las ecuaciones con raíces requieren eliminar la raíz para simplificar la ecuación. Esto se logra elevando ambos lados al exponente que “anula” la raíz.
- Si la ecuación tiene una raíz cuadrada, se eleva ambos lados al cuadrado para eliminarla.
- Para raíces cúbicas, se eleva ambos lados al cubo.
- Después de quitar la raíz, se resuelve la ecuación resultante.
- Es fundamental verificar las soluciones obtenidas, ya que al elevar al cuadrado pueden aparecer soluciones extraviadas (soluciones que no satisfacen la ecuación original).
Ejemplo Práctico Integrado
Consideremos la ecuación:
√(x²/4) + 1/2 = 3
Pasos para resolverla:
- Multiplicamos toda la ecuación por 2 para eliminar la fracción: 2√(x²/4) + 1 = 6
- Despejamos la raíz: 2√(x²/4) = 5
- Dividimos ambos lados por 2: √(x²/4) = 5/2
- Elevamos al cuadrado para eliminar la raíz: x²/4 = (5/2)² = 25/4
- Multiplicamos ambos lados por 4: x² = 25
- Despejamos x: x = ±5
Una vez obtenidas las soluciones, se recomienda sustituirlas en la ecuación original para confirmar que sean correctas.
Paso a paso para simplificar fracciones, exponentes y radicales en ecuaciones
Cuando nos enfrentamos a ecuaciones que involucran fracciones, potencias y raíces, la clave está en aplicar una metodología clara y ordenada para evitar errores y simplificar el proceso.
1. Simplificación de fracciones
El primer paso es simplificar las fracciones algebraicas para reducir la complejidad. Esto incluye:
- Factorizar numerador y denominador
- Cancelar términos comunes
- Convertir fracciones mixtas en fracciones impropias si es necesario
Ejemplo concreto: Simplificá la fracción $$frac{6x^2 – 12x}{3x}$$.
Primero factorizamos el numerador: 6x(x – 2), y el denominador es 3x. Entonces:
$$frac{6x(x-2)}{3x} = 2(x-2)$$, siempre y cuando x neq 0.
2. Manejo de exponentes
Para tratar con potencias, es fundamental dominar las reglas de los exponentes:
- Producto de potencias: $$a^m cdot a^n = a^{m+n}$$
- Cociente de potencias: $$frac{a^m}{a^n} = a^{m-n}$$
- Potencia de potencia: $$(a^m)^n = a^{m cdot n}$$
- Potencia de un producto: $$(ab)^n = a^n b^n$$
Consejo práctico: Siempre que puedas, expresá exponentes negativos como potencias positivas para facilitar el cálculo.
Ejemplo: Simplificá $$frac{x^4 cdot x^{-2}}{x^3}$$.
Aplicando las reglas:
$$frac{x^{4 + (-2)}}{x^3} = frac{x^{2}}{x^{3}} = x^{2 – 3} = x^{-1} = frac{1}{x}$$.
3. Simplificación de radicales
Para los radicales o raíces, existen técnicas específicas que permiten simplificarlos:
- Factorizar el radicando para extraer factores cuadrados o potencias perfectas.
- Utilizar la propiedad $$sqrt[n]{a^m} = a^{frac{m}{n}}$$ para convertir raíces en potencias fraccionarias.
- Racionalizar el denominador cuando sea necesario.
Ejemplo: Simplificá $$sqrt{50}$$.
Factorizamos:
$$sqrt{50} = sqrt{25 times 2} = sqrt{25} times sqrt{2} = 5sqrt{2}$$.
Comparación rápida: exponentes y radicales
| Concepto | Ejemplo | Equivalencia |
|---|---|---|
| Raíz cuadrada | $$sqrt{a}$$ | $$a^{frac{1}{2}}$$ |
| Raíz cúbica | $$sqrt[3]{a}$$ | $$a^{frac{1}{3}}$$ |
| Potencia con exponente fraccionario | $$a^{frac{m}{n}}$$ | $$sqrt[n]{a^m}$$ |
4. Integración en la resolución de ecuaciones
Al simplificar fracciones, exponentes y radicales, el objetivo es dejar la ecuación en una forma más sencilla para despejar la variable.
Ejemplo práctico:
Resolvamos la ecuación:
$$frac{2x^3}{4x} = sqrt{16}$$
Primero simplificamos el lado izquierdo:
$$frac{2x^3}{4x} = frac{2}{4} cdot frac{x^3}{x} = frac{1}{2} x^{3-1} = frac{1}{2} x^{2}$$
El lado derecho es:
$$sqrt{16} = 4$$
Entonces la ecuación es:
$$frac{1}{2} x^{2} = 4$$
Multiplicamos ambos lados por 2:
$$x^{2} = 8$$
Finalmente, aplicamos la raíz cuadrada:
$$x = pm sqrt{8} = pm 2sqrt{2}$$
¡Listo! De esta forma, simplificando paso a paso, resolver ecuaciones con fracciones, potencias y raíces es mucho más accesible y sencillo.
Preguntas frecuentes
¿Cómo simplifico una fracción antes de resolver una ecuación?
Dividí numerador y denominador por su máximo común divisor para obtener la fracción en su forma más simple.
¿Qué hago si la ecuación tiene potencias con exponentes negativos?
Convertí la potencia con exponente negativo a una fracción con exponente positivo invirtiendo la base.
¿Cómo manejo las raíces en una ecuación para facilitar su resolución?
Elevá ambos lados de la ecuación a la potencia correspondiente para eliminar la raíz, siempre verificando las soluciones.
¿Es necesario verificar las soluciones después de resolver la ecuación?
Sí, algunas transformaciones pueden generar soluciones extrañas que no cumplen la ecuación original.
¿Puedo combinar fracciones con exponentes en una misma ecuación?
Sí, siempre que simplifiques cada término y uses las propiedades de los exponentes para combinarlos correctamente.
| Paso | Descripción | Consejo útil |
|---|---|---|
| 1 | Simplificar fracciones | Buscá el máximo común divisor para simplificar términos. |
| 2 | Aplicar propiedades de potencias | Recordá que a^m * a^n = a^{m+n} y (a^m)^n = a^{mn}. |
| 3 | Eliminar raíces | Elevá ambos lados de la ecuación a la potencia adecuada para deshacer la raíz. |
| 4 | Reducir términos semejantes | Sumá o restá fracciones sólo si tienen igual denominador. |
| 5 | Despejar la incógnita | Multiplicá o dividí para aislar la variable en un lado. |
| 6 | Verificar soluciones | Reemplazá los valores encontrados en la ecuación original. |
¿Te quedó alguna duda? Dejá tu comentario abajo y no te olvides de revisar otros artículos en nuestra web que seguro te van a interesar.