Cómo Resolver Ejercicios de Ecuación de la Recta que Pasa por Dos Puntos ✅

✅ Descubrí el método infalible para resolver ecuaciones de la recta entre dos puntos: ¡usá la fórmula punto-pendiente y dominá el álgebra!

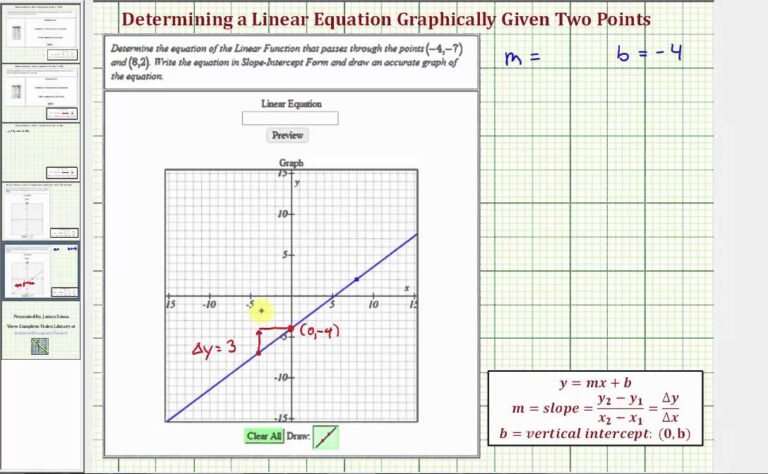
Para resolver ejercicios de ecuación de la recta que pasa por dos puntos, es fundamental conocer la fórmula que permite calcular la pendiente de la recta y luego, a partir de esta, obtener la ecuación en su forma general o punto-pendiente. El proceso comienza identificando las coordenadas de los dos puntos dados, calculando la pendiente con la fórmula m = (y2 – y1) / (x2 – x1), y finalmente utilizando la forma y – y1 = m(x – x1) para escribir la ecuación de la recta.

En este artículo desglosaremos paso a paso cómo llevar adelante esta resolución, ejemplificando cada etapa para que puedas aplicarlo con cualquier par de puntos que te propongan. Veremos cómo interpretar correctamente la fórmula de la pendiente, cómo manipular la ecuación punto-pendiente y cómo convertirla a la forma general o explícita, según el requerimiento. Además, analizaremos casos especiales, como cuando la pendiente es cero o está indefinida, para que puedas dominar este tipo de ejercicios sin dificultades.

Pasos para resolver la ecuación de la recta que pasa por dos puntos

Identificar las coordenadas de los dos puntos: Supongamos que los puntos son P1 (x1, y1) y P2 (x2, y2).
Calcular la pendiente (m):
La pendiente indica la inclinación de la recta y se calcula con la fórmula:
m = (y2 – y1) / (x2 – x1)
Es importante destacar que si x2 = x1, la pendiente es indefinida y la recta es vertical.
Aplicar la fórmula punto-pendiente: Usar uno de los puntos (generalmente P1) en la ecuación:

y – y1 = m(x – x1)

Esto genera la ecuación de la recta en forma punto-pendiente.

Cómo Resolver Ejercicios Prácticos Del Teorema Del Resto

Ejemplo práctico

Consideremos los puntos P1 (2, 3) y P2 (5, 11):

Calcular pendiente:

m = (11 – 3) / (5 – 2) = 8 / 3 ≈ 2.67

Usar punto-pendiente con P1 (2, 3):

y – 3 = (8/3)(x – 2)

Para dejarla en forma explícita (y = mx + b):

y = (8/3)x – (16/3) + 3 = (8/3)x – (16/3) + (9/3) = (8/3)x – (7/3)

Casos especiales a considerar

Recta vertical: Si los dos puntos tienen la misma coordenada x, la ecuación será x = x1.
Recta horizontal: Si los dos puntos tienen la misma coordenada y, la pendiente es cero y la ecuación es y = y1.

Recomendaciones para resolver ejercicios

Verifica siempre que los puntos no sean iguales, porque no se puede definir una recta con un solo punto.
Realiza operaciones con fracciones con cuidado para evitar errores en la pendiente.
Practica con diferentes pares de puntos para familiarizarte con la conversión entre formas de la ecuación de la recta.

Paso a Paso para Determinar la Ecuación de la Recta a partir de Dos Coordenadas

Para resolver ejercicios relacionados con la ecuación de la recta que pasa por dos puntos, es fundamental conocer el procedimiento que nos permite obtener la fórmula matemática que describe esa recta. A continuación, te presentamos un paso a paso claro y efectivo para que puedas aplicarlo en cualquier situación.

1. Identificar los puntos dados

Supongamos que tenemos dos puntos: P₁ (x₁, y₁) y P₂ (x₂, y₂). Por ejemplo, P₁ (2, 3) y P₂ (5, 11).

2. Calcular la pendiente (m)

La pendiente es una medida de la inclinación de la recta y se calcula con la fórmula:

m = (y₂ – y₁) / (x₂ – x₁)

Para nuestro ejemplo:

m = (11 – 3) / (5 – 2) = 8 / 3

Cómo Resolver Ecuaciones De Primer Grado Con Una Incógnita Fácilmente

Este valor nos indica que por cada 3 unidades que avanzamos en x, la recta sube 8 unidades en y.

3. Utilizar la fórmula punto-pendiente

Una vez que tenemos la pendiente, usamos la fórmula punto-pendiente para obtener la ecuación:

y – y₁ = m(x – x₁)

Con nuestro ejemplo, tomando el punto P₁:

y – 3 = (8/3)(x – 2)

4. Desarrollar y simplificar

Para obtener la ecuación en forma explícita (y = mx + b), expandimos y despejamos:

y – 3 = (8/3)x – (16/3)
y = (8/3)x – (16/3) + 3
y = (8/3)x – (16/3) + (9/3) = (8/3)x – (7/3)

Así, la ecuación de la recta es:

y = (8/3)x – (7/3)

Consejos prácticos para evitar errores comunes

Verificar que x₂ ≠ x₁, porque si son iguales, la recta es vertical y la pendiente no está definida.
Utilizar siempre puntos correctos y ordenados (x, y).
Reducir las fracciones para simplificar la pendiente y la ecuación final.

Comparación de formas comunes de la ecuación de la recta

Forma	Expresión	Características	Ejemplo con m=8/3 y punto (2,3)
Pendiente-punto	y – y₁ = m(x – x₁)	Útil para obtener la ecuación rápidamente a partir de un punto y la pendiente.	y – 3 = (8/3)(x – 2)
Forma explícita	y = mx + b	Fácil para graficar y entender la pendiente y la ordenada al origen.	y = (8/3)x – (7/3)
Forma general	Ax + By + C = 0	Útil para ciertos análisis algebraicos y comprobaciones.	8x – 3y – 7 = 0

Ejemplo adicional para practicar

Dados los puntos A(1, 4) y B(3, 10), determina la ecuación de la recta:

Calcula la pendiente: m = (10 – 4) / (3 – 1) = 6 / 2 = 3
Aplica la fórmula punto-pendiente con A: y – 4 = 3(x – 1)
Desarrolla: y – 4 = 3x – 3 → y = 3x + 1

¡Listo! Ya tenés la ecuación. Fácil y rápido.

Preguntas frecuentes

¿Cómo se encuentra la pendiente de una recta que pasa por dos puntos?

Se calcula con la fórmula m = (y2 – y1) / (x2 – x1), donde (x1, y1) y (x2, y2) son los dos puntos dados.

A Cuántos Kilómetros Equivale Una Milla Y Cómo Se Convierte

¿Qué forma tiene la ecuación de la recta que pasa por dos puntos?

Se puede usar la forma punto-pendiente: y – y1 = m(x – x1), donde m es la pendiente y (x1, y1) es uno de los puntos.

¿Qué hago si los dos puntos tienen la misma abscisa?

La recta es vertical y su ecuación es x = x1, donde x1 es la abscisa común de ambos puntos.

¿Cómo se verifica que la ecuación es correcta?

Se reemplazan ambos puntos en la ecuación y se comprueba que satisfacen la igualdad.

¿Puedo usar la forma general de la ecuación de la recta?

Sí, se puede expresar como Ax + By + C = 0, derivando a partir de la forma punto-pendiente.

Puntos clave para resolver ecuaciones de la recta que pasa por dos puntos

Identificar las coordenadas de los dos puntos: (x1, y1) y (x2, y2).
Calcular la pendiente: m = (y2 – y1) / (x2 – x1).
Si x2 = x1, la recta es vertical y la ecuación es x = x1.
Usar la fórmula punto-pendiente: y – y1 = m(x – x1).
Desarrollar la ecuación para obtener la forma explícita: y = mx + b.
Verificar que ambos puntos satisfacen la ecuación final.
Opcional: convertir a la forma general Ax + By + C = 0.
Recordar que la pendiente indica la inclinación de la recta.
Practicar con distintos pares de puntos para afianzar el método.
En caso de dudas, consultar tablas de pendientes o ejemplos resueltos.

¡Dejá tus comentarios abajo y no te pierdas otros artículos de nuestra web que te ayudarán a profundizar en matemáticas y geometría!

Cómo Resolver Ejercicios de Ecuación de la Recta que Pasa por Dos Puntos