✅ La distancia entre dos puntos se calcula aplicando la fórmula de la raíz cuadrada de la suma de los cuadrados de sus diferencias: ¡potencia matemática!
Para calcular la distancia entre dos puntos en el plano cartesiano, se utiliza la fórmula derivada del teorema de Pitágoras. Dada la coordenada de dos puntos, por ejemplo, P1(x1, y1) y P2(x2, y2), la distancia d entre ellos se calcula con la fórmula:
d = √[(x2 – x1)² + (y2 – y1)²].
Esta fórmula permite encontrar la longitud del segmento de línea recta que une ambos puntos en un plano, considerando las diferencias en sus coordenadas horizontales y verticales. A continuación, detallaremos paso a paso cómo aplicar esta fórmula y algunos ejemplos prácticos para que puedas entender y calcular la distancia de manera sencilla.
Desarrollo del cálculo de la distancia entre dos puntos
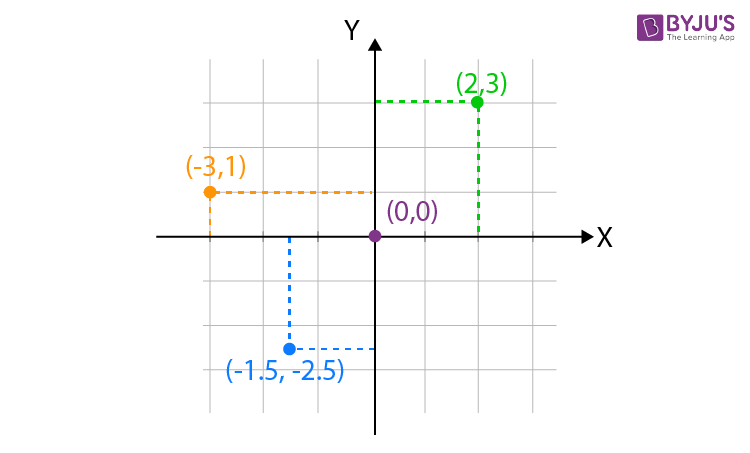
Para entender cómo se llega a esta fórmula, es útil pensar en el plano cartesiano como un sistema de ejes perpendiculares: el eje x (horizontal) y el eje y (vertical). Si tenemos dos puntos P1(x1, y1) y P2(x2, y2), la distancia entre ellos es la hipotenusa de un triángulo rectángulo formado por:
- La diferencia horizontal entre los puntos: |x2 – x1|
- La diferencia vertical entre los puntos: |y2 – y1|
Por el teorema de Pitágoras, el cuadrado de la hipotenusa (la distancia entre los puntos) es igual a la suma de los cuadrados de los catetos (las diferencias horizontales y verticales). Por eso, la fórmula de distancia se expresa como:
d = √[(x2 – x1)² + (y2 – y1)²]
Ejemplo práctico
Supongamos que queremos calcular la distancia entre los puntos P1(2, 3) y P2(7, 11):
- Calculamos la diferencia en x: 7 – 2 = 5
- Calculamos la diferencia en y: 11 – 3 = 8
- Elevamos al cuadrado cada diferencia: 5² = 25 y 8² = 64
- Sumamos los cuadrados: 25 + 64 = 89
- Aplicamos la raíz cuadrada: √89 ≈ 9.43
Por lo tanto, la distancia entre los puntos P1 y P2 es aproximadamente 9.43 unidades.
Fórmula matemática paso a paso para obtener la distancia entre puntos
Para calcular la distancia entre dos puntos en un plano cartesiano, es fundamental entender la estructura del plano y cómo se ubican los puntos mediante coordenadas. Cada punto se representa como un par ordenado (x, y), donde x es la coordenada horizontal y y la vertical.
Supongamos que tenemos dos puntos P₁ (x₁, y₁) y P₂ (x₂, y₂). La distancia entre ellos se calcula usando el teorema de Pitágoras aplicando la siguiente fórmula:
Fórmula de la distancia
d = √[(x₂ – x₁)² + (y₂ – y₁)²]
Desglose paso a paso
- Calculá la diferencia horizontal: Restar las coordenadas x de ambos puntos, es decir, Δx = x₂ – x₁.
- Calculá la diferencia vertical: Restar las coordenadas y, o sea, Δy = y₂ – y₁.
- Elevá al cuadrado ambas diferencias: Esto elimina valores negativos y prepara los términos para la raíz, dando (Δx)² y (Δy)².
- Sumá los cuadrados de las diferencias: (Δx)² + (Δy)².
- Aplicá la raíz cuadrada: Para obtener la distancia directa entre los puntos, calculamos √[(Δx)² + (Δy)²].
Ejemplo práctico
Consideremos los puntos A (3, 4) y B (7, 1):
- Δx = 7 – 3 = 4
- Δy = 1 – 4 = -3 (lo importante es el valor absoluto al elevar al cuadrado)
- (Δx)² = 4² = 16
- (Δy)² = (-3)² = 9
- Sumamos: 16 + 9 = 25
- Raíz cuadrada de 25 = 5
Por lo tanto, la distancia entre A y B es 5 unidades.
¿Por qué es útil esta fórmula?
- Facilita el cálculo directo sin necesidad de gráficos.
- Es aplicable en múltiples campos, desde la física hasta la programación y la ingeniería.
- Permite medir distancias reales en mapas o planos, incluso en coordenadas con valores negativos o decimales.
Consejo práctico:
Cuando trabajes con coordenadas decimales o negativas, no te olvides de respetar los signos en las restas antes de elevarlos al cuadrado. La fórmula se encarga de manejar estos valores para que el resultado siempre sea positivo y correcto.
Comparación con otras métricas
Aunque la fórmula de distancia euclidiana es la más común, en ciertos contextos usan otras métricas, como la distancia de Manhattan o la distancia Chebyshev. Aquí una tabla comparativa:
| Tipo de Distancia | Fórmula | Uso común |
|---|---|---|
| Euclidiana | d = √[(x₂ – x₁)² + (y₂ – y₁)²] | Distancia directa “en línea recta” |
| Manhattan | d = |x₂ – x₁| + |y₂ – y₁| | Rutas en cuadrícula (como calles en una ciudad) |
| Chebyshev | d = max(|x₂ – x₁|, |y₂ – y₁|) | Movimientos en tablero de ajedrez |
Preguntas frecuentes
¿Qué fórmula se usa para calcular la distancia entre dos puntos?
Se utiliza la fórmula de distancia: d = √((x2 – x1)² + (y2 – y1)²).
¿Qué representan x1, y1, x2 y y2 en la fórmula?
Son las coordenadas de los dos puntos; (x1, y1) para el primer punto y (x2, y2) para el segundo.
¿Se puede calcular la distancia en un espacio de más de dos dimensiones?
Sí, la fórmula se extiende sumando las diferencias al cuadrado de cada dimensión y luego sacando la raíz.
¿Qué unidades se usan para medir la distancia?
Depende del sistema de coordenadas, puede ser cualquier unidad como metros, centímetros o unidades arbitrarias.
¿Para qué sirve calcular esta distancia?
Se usa en geometría, física, informática y muchas otras áreas para determinar separación o longitud entre puntos.
Puntos clave para calcular la distancia entre dos puntos en el plano cartesiano
- Identificar las coordenadas de ambos puntos (x1, y1) y (x2, y2).
- Aplicar la fórmula: d = √((x2 – x1)² + (y2 – y1)²).
- Calcular las diferencias: Δx = x2 – x1 y Δy = y2 – y1.
- Elevar al cuadrado las diferencias: (Δx)² y (Δy)².
- Sumar los cuadrados: (Δx)² + (Δy)².
- Extraer la raíz cuadrada del resultado para obtener la distancia.
- Interpretar la distancia en la unidad correspondiente.
- Recordar que esta fórmula proviene del teorema de Pitágoras.
- Se puede representar gráficamente para mejor comprensión.
- Extensión posible a 3D y más dimensiones sumando más términos.
¿Te resultó útil esta explicación? ¡Dejanos tus comentarios y no te pierdas otros artículos de nuestra web que también pueden interesarte!