✅ Para construir una gráfica lineal desde una ecuación, identificá la pendiente y la ordenada al origen, trazá el eje y marcá los puntos clave.
Construir una gráfica lineal a partir de una ecuación es un proceso fundamental en matemáticas que consiste en representar visualmente la relación entre dos variables. Para ello, se utiliza la forma general de la ecuación lineal, por ejemplo, y = mx + b, donde m es la pendiente y b es la ordenada al origen. Este método permite interpretar fácilmente cómo varía una variable en función de la otra.
En este artículo te explicaremos paso a paso cómo construir una gráfica lineal a partir de una ecuación, detallando cada elemento que debes considerar y el procedimiento para obtener los puntos que formarán la línea. Así, podrás entender no solo cómo dibujar la gráfica, sino también interpretar el significado de la pendiente y la intersección con el eje vertical.
1. Identificar la forma de la ecuación
La ecuación lineal más común es y = mx + b, donde:
- m: pendiente de la recta, indica la inclinación y dirección de la línea.
- b: ordenada al origen, es el punto donde la línea cruza el eje y.
Si la ecuación no está en esta forma, conviene despejar y para obtenerla.
2. Graficar el punto de intersección (ordenada al origen)
Localizá el número b en el eje y y marcá ese punto. Por ejemplo, si la ecuación es y = 2x + 3, el punto será (0,3).
3. Utilizar la pendiente para obtener otro punto
La pendiente m representa el cambio en y por unidad de cambio en x. Por ejemplo, si m = 2, significa que por cada 1 unidad que aumenta x, y aumenta 2 unidades.
Partiendo del punto (0, b), movete según la pendiente: si m = frac{rise}{run}, subí o bajá «rise» unidades y corré «run» unidades hacia la derecha para encontrar otro punto. Por ejemplo, para m = frac{3}{2}, subí 3 y corré 2 hacia la derecha.
4. Dibujar la línea
Conectá los puntos que obtuviste con una regla para formar la línea recta que representa la ecuación.
5. Verificar con un tercer punto (opcional)
Para confirmar que la gráfica es correcta, podés calcular un tercer punto sustituyendo otro valor de x en la ecuación y chequeando que ese punto esté sobre la línea.
Ejemplo práctico
Digamos que tenés la ecuación y = -frac{1}{2}x + 4.
- El punto de intersección es (0,4).
- La pendiente es -1/2, por lo que desde (0,4), bajás 1 unidad y corrés 2 unidades a la derecha para obtener el punto (2,3).
- Dibujás la línea que pasa por ambos puntos.
Siguiendo estos pasos, podés construir cualquier gráfica lineal de forma clara y precisa.
Paso a paso para identificar los valores de x e y en la ecuación
Cuando queremos construir una gráfica lineal a partir de una ecuación, el primer paso fundamental es identificar correctamente los valores de x y y. Esto nos permitirá representar puntos en el plano cartesiano y, a partir de ellos, trazar la línea que describe la función.
¿Qué son los valores de x e y en una ecuación lineal?
En una ecuación lineal de la forma y = mx + b, x es la variable independiente, mientras que y es la variable dependiente. Esto significa que los valores de y dependen directamente de los valores que elijamos para x.
Ejemplo concreto
Consideremos la ecuación y = 2x + 3. Si queremos encontrar valores que nos ayuden a graficar:
- Si x = 0, y = 2(0) + 3 = 3
- Si x = 1, y = 2(1) + 3 = 5
- Si x = -1, y = 2(-1) + 3 = 1
Estos pares ordenados (x, y) se convierten en puntos que ubicamos en el plano cartesiano.
Recomendaciones para elegir valores de x
- Elegí valores de x que estén cerca del origen para facilitar la representación gráfica.
- Usá valores enteros para simplificar el cálculo y la ubicación de puntos.
- Probá con valores negativos y positivos para obtener una mejor perspectiva de la gráfica.
Tabla de valores para graficar la ecuación y = 2x + 3
| x | y = 2x + 3 |
|---|---|
| -2 | -1 |
| -1 | 1 |
| 0 | 3 |
| 1 | 5 |
| 2 | 7 |
Consejo práctico
Para evitar errores comunes, siempre verificá tus cálculos antes de graficar los puntos, y recordá que cada valor de x debe tener un único valor de y asociado para que la gráfica sea correcta.
Casos de uso
- Educación: Enseñar a los estudiantes a identificar valores de x y y es clave para comprender funciones lineales y su representación gráfica.
- Economía: Graficar funciones de costo o ingreso donde x representa cantidad y y el costo o ingreso total.
- Ingeniería: Análisis de sistemas lineales donde variables dependen de otras para modelar procesos o fenómenos.
Preguntas frecuentes
¿Qué es una gráfica lineal?
Una gráfica lineal representa una función lineal, mostrando la relación entre dos variables mediante una línea recta.
¿Cómo se identifica la pendiente en una ecuación lineal?
La pendiente es el coeficiente de la variable x en la forma y = mx + b, donde m indica la inclinación de la recta.
¿Qué significa el término independiente en la ecuación?
Es el valor b en y = mx + b, que indica dónde la línea corta el eje y (ordenadas).
¿Cómo se obtienen los puntos para graficar?
Se sustituyen valores de x en la ecuación para calcular los correspondientes valores de y y así obtener puntos para graficar.
¿Qué herramientas puedo usar para graficar fácilmente?
Se puede usar papel milimetrado, calculadoras gráficas o programas como GeoGebra y Excel.
¿Para qué sirven las gráficas lineales?
Permiten visualizar relaciones lineales, predecir valores y analizar comportamientos entre variables.
Puntos clave para construir una gráfica lineal a partir de una ecuación
- Identificar la forma de la ecuación: y = mx + b.
- Determinar la pendiente (m) para conocer la inclinación.
- Identificar el término independiente (b) para el punto de intersección con el eje y.
- Elegir varios valores de x y calcular sus correspondientes valores de y.
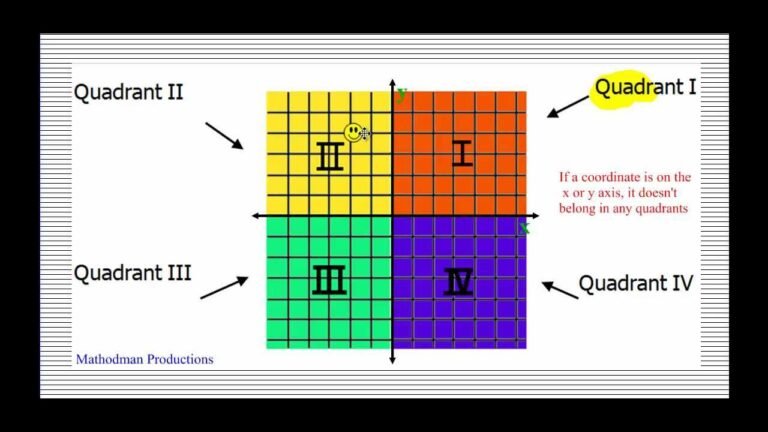
- Marcar los puntos (x, y) en el plano cartesiano.
- Unir los puntos con una línea recta que se extienda en ambas direcciones.
- Verificar que la pendiente de la línea corresponda con la pendiente calculada.
- Utilizar escalas adecuadas en ambos ejes para facilitar la lectura.
- Si la pendiente es positiva, la línea sube de izquierda a derecha; si es negativa, baja.
- El eje x representa la variable independiente; el eje y, la dependiente.
Dejá tus comentarios abajo y no te pierdas otros artículos relacionados en nuestra web para seguir aprendiendo sobre matemáticas y gráficos.