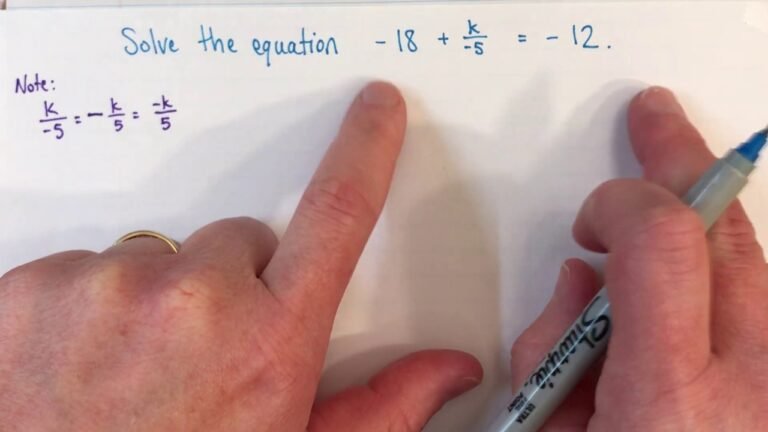✅ Para despejar X en ecuaciones con fracciones, igualá denominadores, simplificá y aislá X usando operaciones inversas paso a paso.
Para despejar la incógnita X en ecuaciones que contienen fracciones, es fundamental seguir un método estructurado que facilite la eliminación de los denominadores y simplifique la resolución del problema. Generalmente, se multiplica ambos lados de la ecuación por el mínimo común denominador (MCD) de todas las fracciones presentes para convertirlas en expresiones sin denominadores, lo que permite luego aislar X de manera directa.
Te explicaremos paso a paso cómo abordar ecuaciones con fracciones para despejar X. Veremos cómo identificar el mínimo común denominador, cómo realizar las operaciones correspondientes y cómo simplificar correctamente la ecuación para llegar al resultado final. Además, incluiremos ejemplos prácticos para que puedas aplicar esta técnica con facilidad.
Pasos para despejar la incógnita X en ecuaciones con fracciones
- Identificar las fracciones presentes en la ecuación y sus denominadores.
- Calcular el mínimo común denominador (MCD) de todas las fracciones para eliminar los denominadores en un solo paso.
- Multiplicar ambos lados de la ecuación por el MCD, lo que convierte todas las fracciones en términos sin denominadores.
- Distribuir el MCD en cada término para simplificar la expresión.
- Agrupar todos los términos que contienen X en un lado de la ecuación y los términos numéricos en el otro.
- Resolver la ecuación resultante que ya no contiene fracciones para despejar la incógnita X.
Ejemplo práctico
Consideremos la siguiente ecuación:
(1/3)X + (2/5) = (4/15)X – (1/2)
1. Identificamos los denominadores: 3, 5, 15 y 2.
2. Calculamos el MCD: El MCD entre 3, 5, 15 y 2 es 30.
3. Multiplicamos toda la ecuación por 30:
- 30 × (1/3)X = 10X
- 30 × (2/5) = 12
- 30 × (4/15)X = 8X
- 30 × (-1/2) = -15
Queda la ecuación:
10X + 12 = 8X – 15
4. Agrupamos términos:
10X – 8X = -15 – 12
2X = -27
5. Despejamos X:
X = -27 / 2
Por lo tanto, X = -13.5.
Consejos para resolver ecuaciones con fracciones
- Verifica siempre los denominadores para evitar errores al calcular el MCD.
- Multiplica cuidadosamente para eliminar las fracciones sin alterar la igualdad.
- Simplifica términos semejantes antes de despejar la incógnita para facilitar el cálculo.
- Revisa tu resultado sustituyendo el valor de X en la ecuación original para asegurarte de que sea correcto.
Pasos detallados para simplificar fracciones y aislar la variable X
Cuando trabajamos con ecuaciones que contienen fracciones, el desafío principal suele ser despejar la incógnita X de manera clara y precisa. Para lograrlo, es fundamental seguir un proceso ordenado y metódico que facilite la simplificación y el aislamiento de la variable.
1. Identificar y simplificar las fracciones
Antes de despejar, es indispensable reducir las fracciones a su forma más simple. Esto no solo mejora la claridad sino que evita errores futuros.
- Ejemplo: Si tienes la fracción 6/8, simplifícala a 3/4 dividiendo numerador y denominador por su máximo común divisor (MCD), en este caso 2.
- Si las fracciones involucran expresiones algebraicas, factoriza y elimina factores comunes.
Consejo práctico:
Usá el MCD para simplificar fracciones numéricas y el factor común para fracciones algebraicas. Esto reduce la complejidad y hace más sencillo el manejo de la ecuación.
2. Eliminar denominadores mediante la multiplicación cruzada
Una vez simplificadas las fracciones, el próximo paso para despejar X es eliminar los denominadores. Esto se puede lograr multiplicando ambos lados de la ecuación por el mínimo común múltiplo (MCM) de los denominadores.
- Ejemplo concreto: Si la ecuación es (2x + 3)/5 = 7/10, identificá que los denominadores son 5 y 10. El MCM es 10.
- Multiplicá ambos lados por 10 para eliminar los denominadores:
10 × (2x + 3)/5 = 10 × 7/10 => 2 × (2x + 3) = 7
3. Desarrollar y simplificar la ecuación resultante
Tras eliminar denominadores, expandí y simplificá la ecuación para dejar a X en un solo lado.
- Siguiendo el ejemplo anterior, distribuí el 2:
2 × (2x + 3) = 7 => 4x + 6 = 7
Luego, restá 6 en ambos lados:
4x + 6 - 6 = 7 - 6 => 4x = 1
4. Aislar la variable X
Finalmente, para despejar X, dividí ambos lados por el coeficiente que acompaña a la variable.
4x = 1 => x = 1/4
Resumen en tabla:
| Paso | Acción | Ejemplo |
|---|---|---|
| 1 | Simplificar fracciones | 6/8 → 3/4 |
| 2 | Multiplicar por MCM para eliminar denominadores | (2x + 3)/5 = 7/10 → 10 × ambos lados |
| 3 | Expandir y simplificar | 4x + 6 = 7 → 4x = 1 |
| 4 | Aislar la variable (dividir coeficiente) | x = 1/4 |
Aplicaciones prácticas
El conocimiento de cómo despejar X en ecuaciones con fracciones es fundamental en áreas como:
- Ingeniería: Cálculo de variables en fórmulas que involucran proporciones.
- Economía: Determinación de precios o cantidades en ecuaciones con tasas y proporciones.
- Física: Resolución de problemas con velocidades, fuerzas y tiempos que se expresan en fracciones.
Dato curioso:
Estudios en educación matemática muestran que aproximadamente un 70% de los estudiantes tienen dificultades para manejar fracciones en ecuaciones, por lo que dominar estos pasos es clave para mejorar su rendimiento y confianza.
Preguntas frecuentes
¿Qué significa despejar la incógnita X?
Despejar la incógnita X implica manipular la ecuación para dejar a X sola en un lado del igual, facilitando así encontrar su valor.
¿Cómo se manejan las fracciones al despejar X?
Se multiplican ambos lados de la ecuación por el denominador para eliminar las fracciones y simplificar la expresión.
¿Puedo despejar X si está en ambos lados de la ecuación?
Sí, primero se agrupan todos los términos con X en un lado y luego se despeja normalmente.
¿Qué hago si la fracción tiene una suma o resta en el denominador?
Es necesario simplificar o eliminar el denominador mediante multiplicación cruzada o multiplicando por el mínimo común denominador.
¿Es importante revisar la solución al final?
Sí, siempre se debe sustituir el valor de X en la ecuación original para verificar que la igualdad se cumple.
| Paso | Descripción | Ejemplo |
|---|---|---|
| 1 | Identificar la ecuación y la incógnita X | (frac{2X + 3}{4} = 5) |
| 2 | Multiplicar ambos lados por el denominador para eliminar la fracción | (4 cdot frac{2X + 3}{4} = 5 cdot 4 Rightarrow 2X + 3 = 20) |
| 3 | Despejar X aislando los términos que lo contienen | Restar 3: (2X = 17) |
| 4 | Dividir para obtener X | (X = frac{17}{2} = 8.5) |
| 5 | Verificar sustituyendo en la ecuación original | (frac{2(8.5) + 3}{4} = frac{17 + 3}{4} = frac{20}{4} = 5) |
Dejanos tus comentarios abajo y no te olvides de revisar otros artículos en nuestra web que pueden interesarte, como Ecuaciones de primer grado paso a paso o Cómo simplificar fracciones algebraicas.