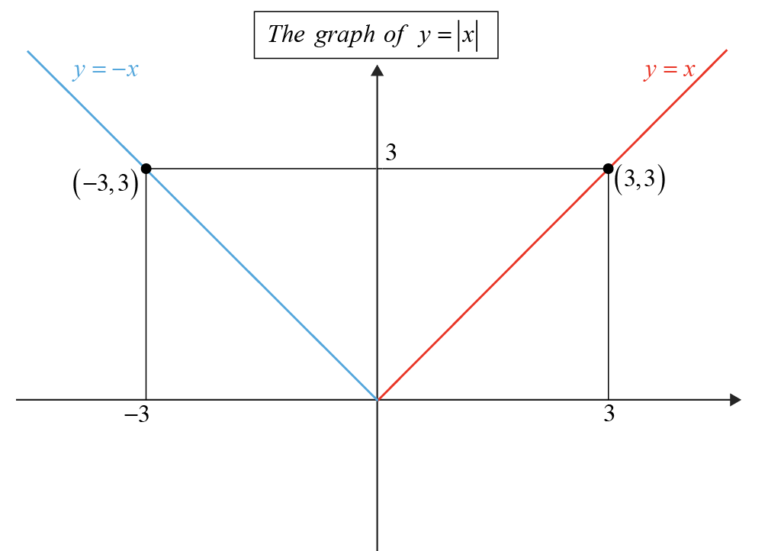
✅ Resolvé desigualdades con valor absoluto aislando el valor absoluto, planteando dos casos, resolviendo cada inecuación y verificando la solución.
Para resolver desigualdades con valor absoluto de manera efectiva, es fundamental entender que el valor absoluto representa la distancia de un número al cero en la recta numérica, siempre como un valor positivo o cero. Por eso, cuando tenemos una desigualdad que involucra valor absoluto, debemos considerar dos casos diferentes que reflejan esa distancia en ambos sentidos (positivo y negativo).
Te explicaremos paso a paso cómo resolver desigualdades con valor absoluto, abordando desde los conceptos básicos hasta ejemplos prácticos y detallados. Aprenderás a transformar la desigualdad en dos casos separados y a interpretar correctamente las soluciones obtenidas.
¿Qué es una desigualdad con valor absoluto?
Una desigualdad con valor absoluto es una expresión matemática donde aparece una función valor absoluto y una desigualdad, por ejemplo: |x – 3| < 5 o |2x + 1| ≥ 7. La clave para resolverlas es descomponerlas en dos desigualdades lineales sin valor absoluto basándonos en la definición de valor absoluto:
- |A| < B equivale a -B < A < B cuando B > 0.
- |A| > B equivale a A < -B o A > B, también para B > 0.
Paso a paso para resolver desigualdades con valor absoluto
- Isolar la expresión con valor absoluto: Si la desigualdad tiene términos adicionales, primero despejar para que el valor absoluto quede solo en un lado.
- Determinar el signo de la constante: Asegurarse que el número sin valor absoluto (por ejemplo, B) sea positivo, ya que el valor absoluto es siempre mayor o igual a cero.
- Dividir la desigualdad en dos casos: Según si la desigualdad es <, ≤, > o ≥, aplicar las reglas para convertir en dos desigualdades lineales.
- Resolver cada desigualdad por separado: Encontrar las soluciones para cada caso.
- Unir las soluciones según la desigualdad: Si es «<" o "≤", la solución es la intersección de los intervalos; si es ">» o «≥», la solución es la unión.
- Comprobar las soluciones: Sustituir valores en la desigualdad original para verificar que cumplan con la condición.
Ejemplo práctico
Resolver la desigualdad: |x – 4| < 3
- La desigualdad |x – 4| < 3 indica que la distancia entre x y 4 es menor que 3.
- Por definición: -3 < x – 4 < 3
- Sumamos 4 en todos los términos para aislar x: 1 < x < 7
- La solución es el intervalo abierto (1, 7), es decir, todos los números mayores que 1 y menores que 7.
Ejemplo con desigualdad mayor o igual
Resolver: |2x + 1| ≥ 5
- Separamos en dos casos:
- 2x + 1 ≥ 5
- 2x + 1 ≤ -5
- Resolver cada desigualdad:
- 2x + 1 ≥ 5 → 2x ≥ 4 → x ≥ 2
- 2x + 1 ≤ -5 → 2x ≤ -6 → x ≤ -3
- La solución es la unión de los intervalos: (-∞, -3] ∪ [2, ∞).
Explicación de los Principios Básicos del Valor Absoluto en Desigualdades
Para comenzar a comprender cómo se resuelven las desigualdades con valor absoluto, primero debemos entender qué es el valor absoluto y cómo afecta a las desigualdades. El valor absoluto de un número representa su distancia al origen cero en la recta numérica, sin importar la dirección. Por ejemplo, el valor absoluto de -5 y 5 es 5.
Definición Matemática
El valor absoluto de un número real x, se denota como |x|, y se define como:
- |x| = x si x ≥ 0
- |x| = -x si x < 0
Esta definición nos dice que el valor absoluto siempre es un número positivo o cero.
¿Cómo se aplican estos principios en las desigualdades?
Las desigualdades con valor absoluto toman la forma general:
|A| < B o |A| > B, donde A es una expresión algebraica y B un número real.
Para resolverlas, se descomponen en dos casos posibles, según la definición del valor absoluto:
- A < B y A > -B si la desigualdad es |A| < B, con B > 0.
- A < -B o A > B si la desigualdad es |A| > B, con B > 0.
Ejemplo concreto para ilustrar
Consideremos la desigualdad |x – 3| < 5. Según los principios, esto se descompone en:
- x – 3 < 5
- x – 3 > -5
Resolviendo ambas:
- x < 8
- x > -2
Por lo tanto, la solución es el intervalo (-2, 8), es decir, todos los valores que están a menos de 5 unidades de distancia de 3.
Consejos prácticos para resolver desigualdades con valor absoluto
- Siempre verifica que B sea positivo antes de aplicar las reglas, ya que el valor absoluto no puede ser menor que un número negativo.
- Resuelve la desigualdad en dos casos: uno considerando A positivo y otro negativo.
- Dibuja la recta numérica para visualizar las soluciones, esto ayuda a confirmar el resultado.
- Utiliza ejemplos numéricos para verificar que la solución cumple la desigualdad original.
Tabla resumen: Principios para resolver desigualdades con valor absoluto
| Tipo de desigualdad | Condición para B | Descomposición en dos casos | Ejemplo |
|---|---|---|---|
| |A| < B | B > 0 |
| |x – 3| < 5 → -2 < x < 8 |
| |A| > B | B > 0 |
| |x + 1| > 4 → x < -5 o x > 3 |
Recordá que entender estos fundamentos es clave para avanzar hacia el manejo de desigualdades más complejas con valor absoluto, que pueden incluir expresiones cuadráticas o sistemas de desigualdades.
Preguntas frecuentes
¿Qué es una desigualdad con valor absoluto?
Es una desigualdad que involucra el valor absoluto de una expresión, es decir, la distancia de un número al cero en la recta numérica.
¿Cómo se resuelve una desigualdad del tipo |x| < a?
Se transforma en una doble desigualdad: -a < x < a, siempre que a sea positivo.
¿Qué pasa si la desigualdad es |x| > a?
Se descompone en dos desigualdades: x < -a o x > a, con a positivo.
¿Qué hago si el valor absoluto está en ambos lados de la desigualdad?
Se deben analizar casos separados, igualando o cambiando el signo dentro del valor absoluto según corresponda.
¿Puedo resolver desigualdades con valor absoluto usando gráficas?
Sí, las gráficas ayudan a visualizar las soluciones y entender los intervalos que cumplen la desigualdad.
¿Qué ocurre si el término a es negativo en |x| < a?
No existen soluciones, porque el valor absoluto siempre es mayor o igual a cero.
Puntos clave para resolver desigualdades con valor absoluto
- Identificar si la desigualdad es estricta (< o >) o no (≤ o ≥).
- Separar la desigualdad en casos según la definición del valor absoluto.
- Para |x| < a con a > 0, resolver como -a < x < a.
- Para |x| > a con a > 0, resolver como x < -a o x > a.
- Si a ≤ 0 en |x| < a, no hay soluciones; en |x| > a, la solución es todo el conjunto real.
- Siempre verificar las soluciones en la desigualdad original para evitar errores.
- Usar gráficos para entender y confirmar intervalos de solución.
- En desigualdades con expresiones más complejas dentro del valor absoluto, plantear casos según el signo de la expresión.
¿Te quedó alguna duda? ¡Dejanos tus comentarios y no te pierdas otros artículos en nuestra web sobre matemáticas y álgebra!